I recently spent three months at OCaml Labs in Cambridge, where I designed and implemented an ahead-of-time compiler from WebAssembly to native code by targeting the Cmm intermediate representation of the OCaml compiler. It was a really enjoyable project!

In this post, I’ll give a brief introduction to WebAssembly and motivate the need for a native code compiler for WebAssembly in the first place, before diving into the more technical details. The compiler passes the WebAssembly test suite in its entirety. I’ll also show some preliminary performance results.

This is joint work with KC Sivaramakrishnan and Stephen Dolan.

WebAssembly

WebAssembly is a new binary format for web applications. The original WebAssembly paper has this wonderful quote:

“By historical accident, JavaScript is the only natively supported programming language on the Web […]”

The JavaScript ecosystem is impressive these days. That said, many people want to write code in a language that isn’t JavaScript (for example, if the remainder of their code is in a different language, or if they are using a specialised web language such as Elm) – and therefore must treat JavaScript as a compilation target.

JavaScript is a high-level scripting language, and is a poor compilation target: its semantics can be eccentric (for example, equality), and even with minification, files are large and verbose.

WebAssembly is designed to replace JavaScript as a compilation target, aiming to provide a language which is:

• Safe
• Fast
• Portable
• Compact

WebAssembly has support across all four major browsers (Chrome, Firefox, Edge, and Safari), and the Emscripten compiler has mature support for compiling C/C++ applications to WebAssembly.

WebAssembly has a few interesting features which set it apart from other bytecodes or languages:

• To provide compact binaries, WebAssembly is a stack machine. So, instead of operations having explicit arguments, they pop their arguments off an implicit operand stack.

• WebAssembly modules are statically typed. The type system is pretty simple: there are four basic types (32 and 64-bit integers and floats), and the typing rules make it possible to statically know the layout of the stack.

• WebAssembly does not allow arbitrary jumps as in regular assembly: instead, WASM provides structured control flow.

• Each WebAssembly module may have a linear memory, which is essentially a big array of bytes. All accesses to the linear memory are bounds-checked.

• WebAssembly is a first-order language, but it allows function pointers to be emulated through the use of a function table.

But compilation from high-level languages to WebAssembly is not what this blog post is about! We’ll be going in the other direction: from WebAssembly to native code.

Wait – WebAssembly TO Native code?

Yes! cmm_of_wasm is a compiler from WebAssembly to native code, via the OCaml backend.

The WebAssembly specification is constantly evolving. While WASM 1.0 has been finalised and released, more advanced language features are in the pipeline, primarily to support compilation from higher-level languages such as Java or C#. Currently, one may prototype these by modifying the reference interpreter – but that is not enough when wanting to evaluate compilation strategies or get performance numbers. The alternative is modifying a browser, which have huge codebases. (As an example, the TaintAssembly project is a pretty heroic effort which adds taint tracking to V8).

There are some excellent other efforts to do standalone native / JIT compilation for WebAssembly. In particular:

• wasm2c is part of the wabt toolkit, and translates from WebAssembly into C code. A key design decision is that the generated C code should look as much like WebAssembly as possible.

• WAVM is a standalone JIT compiler for WebAssembly via LLVM.

cmm_of_wasm puts a more functional spin on WASM compilation. Currently, it needs a slightly-patched version of OCaml to compile.

In the longer term, we hope to show type- and semantics-preserving translations from WebAssembly to each of the 2 IRs we use and then down to Cmm, getting us closer to showing verified WebAssembly compilation.

Why OCaml?

So, why the OCaml backend, and not JVM bytecode, LLVM, or x86 assembly?

This is a good question. There are a few answers: we were worried about overzealous optimisations which would contravene the WebAssembly specification, such as elimination of redundant loads; there was plenty of deep local expertise available; the Cmm backend seemed to be at a level of abstraction high enough for us to define very structured translations but low enough to support operations such as memory accesses; and eventually we hope to hook into OCaml’s excellent garbage collector.

That said, hopefully some of the IR wrangling we’ve done should be of some use more generally.

The Compiler

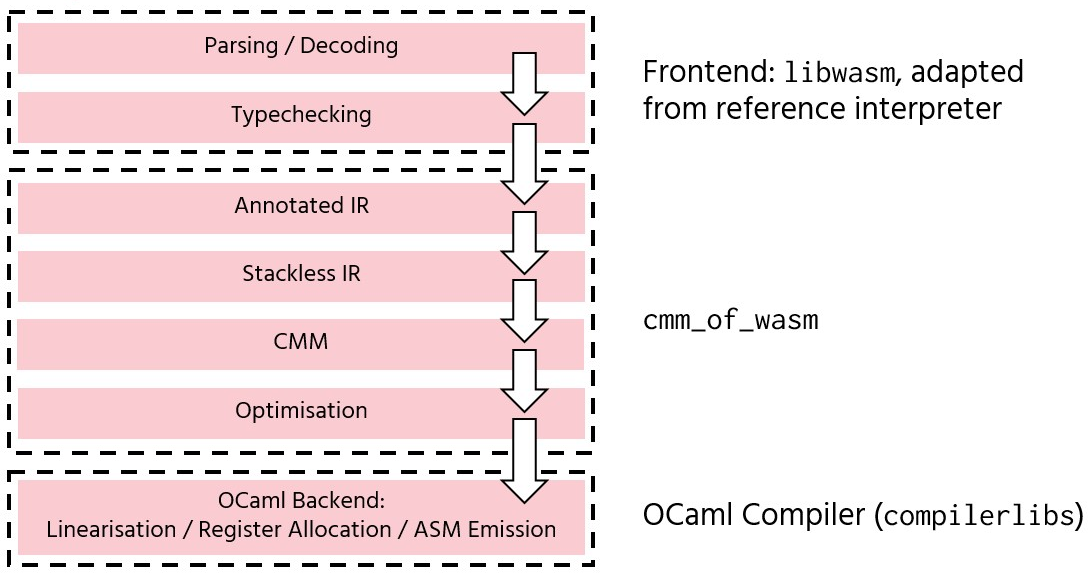
The compiler can roughly be divided into three phases:

1. libwasm: A repackaging of the reference interpreter. Provides parsing, binary manipulation, and typechecking.

2. cmm_of_wasm: The main novel part of the compiler, which translates away the WebAssembly operand stack and generates Cmm code.

3. The OCaml backend: From Cmm, performs register allocation, a few low-level optimisations, and generates native object code.

We also generate “C stubs” to bridge the OCaml and C calling conventions, and generate header files so that the object files may be linked with C programs.

We’ll now do a bit more of a deep dive into the two intermediate representations (Annotated and Stackless), before looking at the translation into Cmm.

A small example

We’ll continue the rest of this post with the example of iteratively calculating the Fibonacci numbers. Recall the definition of the Fibonacci numbers:

fib(0) = 0
fib(1) = 1
fib(n) = fib(n - 2) + fib(n - 1)

A simple recursive definition of this is horrendously inefficient, however the nth Fibonacci number may be calculated iteratively using linear time and constant space. (I realise that there’s a closed-form solution, but that makes for a less interesting example!)

Let’s see an example of this in C:

int fib_iter(int n) {
  int counter = 2;
  int i1 = 0;
  int i2 = 1;
  int tmp = 0;

  if (n == 0) {
    return 0;
  }

  if (n == 1) {
    return 1;
  }

  while (counter < n) {
    tmp = i1 + i2;
    i1 = i2;
    i2 = tmp;
    counter++;
  }

  return i1 + i2;
}

I realise that this isn’t hugely idiomatic C – a for loop would be better; we should assert that n > 0; and the temporary variable would be declared in the loop, and so on – but bear with me as these decisions make it easier to draw comparisons with the WASM.

We define a parameter n; a counter which we initially set to 2; i1 which is the previously-calculated fib(n-2) and i2 which is the previously-calculated fib(n-1); and a temporary variable tmp which is used when swapping fib(n-1) and fib(n-2).

The algorithm works as follows:

• Check the special cases for fib(0) and fib(1)
• If counter is less than the parameter n, then use the previously-calculated fib(n-2) and fib(n-1) values to calculate fib(n). Set i1 to fib(n-1), set i2 to fib(n), increment counter and repeat.
• Otherwise, return fib(n-2) + fib(n-1) using the stored values.

Now, let’s have a look at the algorithm in WebAssembly. Note that while WASM is a bytecode and is generally machine-generated, this WASM is hand-written using the textual S-Expression representation.

(func (export "fib_iter")
  (param i64) ;; Local 0 (parameter): Target
  (result i64) ;; Result is a 64-bit integer
  (local i64) ;; Local 1: counter
  (local i64) ;; Local 2: i1
  (local i64) ;; Local 3: i2
  (local i64) ;; Local 4: tmp

  (set_local 2 (i64.const 0)) ;; i1 = 0
  (set_local 3 (i64.const 1)) ;; i2 = 1

  ;; if (n == 0) { return 0; }
  (if (i64.eq (get_local 0) (i64.const 0))
    (then (return (i64.const 0))))

  ;; if (n == 1) { return 1; }
  (if (i64.eq (get_local 0) (i64.const 1))
    (then (return (i64.const 1))))

  ;; counter = 2;
  (set_local 1 (i64.const 2))

  ;; while (counter < n)
  (loop
    (if (i64.lt_s (get_local 1) (get_local 0))
      (then
        ;; tmp = i1 + i2;
        (set_local 4 (i64.add (get_local 2) (get_local 3)))
        ;; i1 = i2;
        (set_local 2 (get_local 3))
        ;; i2 = tmp;
        (set_local 3 (get_local 4))
        ;; counter++;
        (set_local 1 (i64.add (get_local 1) (i64.const 1)))
        ;; continue looping
        (br 1))
    )
  )
  ;; return i1 + i2;
  (return (i64.add (get_local 2) (get_local 3)))
)

Each bit of WASM is commented with the C code it corresponds to. A few things are worth mentioning. Firstly, WASM requires the parameters and local variables all to be declared upfront. The indexing space begins with the parameters, and is followed by each local variable. Therefore, we have that n is index 0, counter is index 1, i1 is 2, i2 is 3, and tmp is 4. All are mutable and can be get or set using get_local and set_local respectively.

It’s worth noting the structured control flow. The br 1 instruction means that “branch to the block with relative nesting depth of 1”. Here, the then block has depth 0 as it is closest, and the loop block has depth 1.

There are two types of blocks: “normal” blocks (as introduced by the block construct, or then in this case), meaning that branching to them will resume execution at the end of the block, and loop blocks, where branching to them will resume execution at the start of the block. Hence, here, evaluating br 1 will cause the loop block to be evaluated again.

The WASM textual representation is designed as syntactic sugar, hiding the fact that WASM is actually a stack machine. Desugared, we get the following WebAssembly function:

(func $0
  ;; Declare local variables
  (local i64 i64 i64 i64)

  ;; i1 = 0;
  (i64.const 0)
  (set_local 2)

  ;; i2 = 1;
  (i64.const 1)
  (set_local 3)

  ;; n == 0: pushes 1 onto the stack if true, 0 otherwise
  (get_local 0)
  (i64.const 0)
  (i64.eq)

  ;; if last value in the stack is nonzero (i.e., conditional
  ;; returned true), return 0
  (if (then (i64.const 0) (return)) (else))

  ;; Similarly, if n == 1, return 1
  (get_local 0)
  (i64.const 1)
  (i64.eq)
  (if (then (i64.const 1) (return)) (else))

  ;; counter = 2
  (i64.const 2)
  (set_local 1)

  ;; Loop
  (loop
    ;; if (counter < n)
    (get_local 1)
    (get_local 0)
    (i64.lt_s)
    (if
      (then
        ;; tmp = i1 + i2;
        (get_local 2)
        (get_local 3)
        (i64.add)
        (set_local 4)

        ;; i1 = i2
        (get_local 3)
        (set_local 2)

        ;; i2 = tmp
        (get_local 4)
        (set_local 3)

        ;; counter++
        (get_local 1)
        (i64.const 1)
        (i64.add)
        (set_local 1)

        ;; continue loop
        (br 1)
      )
      (else)
    )
  )

  ;; return (i1 + i2);
  (get_local 2)
  (get_local 3)
  (i64.add)
  (return)
)

The file is similar, but instead of

(i64.add (get_local 2) (get_local_3))

the desugared form shows how the WASM bytecode is actually stored, where local variable 2 and local variable 3 are pushed onto the stack as arguments to the i64.add operator.

(get_local 2)
(get_local 3)
(i64.add)

Annotated IR

The annotated IR is a fairly uninteresting intermediate representation which annotates each block with the local variables that are modified inside of it, including any sub-blocks. This is useful for when we later compile away local variables into single static assignment (SSA) form. The Annotated IR can be calculated efficiently in a single pass.

Stackless IR

The Stackless IR is where things become more interesting. While a stack machine allows compact storage of WASM programs, it’s more challenging to compile it directly. Additionally, thinking about block nesting levels becomes cumbersome, and having mutable local variables floating around makes optimisations (such as constant folding) trickier.

The Stackless IR has:

• No operand stack: everything is explicitly let-bound, and operations take arguments explicitly
• No mutable variables: the IR is in single-static assignment form
• Explicit continuations

If you are unfamiliar with continuations, they can be thought of as “a bit of the program that can be evaluated later”. Consider the following example, where we compare two numbers, returning 1 if they are equal and 2 otherwise. In WebAssembly, we could write:

(func $compare (param $i1 i64) (param $i2 i64) (result i64) (local $res i64)
  (get_local $i1)
  (get_local $i2)
  (i64.eq)
  (if
    (then (set_local $res (i64.const 1)))
    (else (set_local $res (i64.const 2))))
  (return (get_local $res))
)

We set the res variable to 1 if the numbers are equal, 2 otherwise, then return res afterwards.

The Stackless representation of the program is:

(fun (param v0:i64) (param v1:i64) (result i64)
  (let v2:i64 = (i64.const 0))
  (let v3:i64 = ((i64.eq) v0:i64 v1:i64))
  (cont(0)(v4:i64) (br return(v4:i64)))
  (cont(1)() (let v5:i64 = (i64.const 1)) (br 0(v5:i64)))
  (cont(2)() (let v6:i64 = (i64.const 2)) (br 0(v6:i64)))
  (if v3:i64 1() 2())
)

There are a few differences. Firstly, the stack is gone completely: we have an explicit let binding construct, i64.eq takes two arguments explicitly, as you would expect in a more traditional language. Secondly, we have constructs of the form cont: let’s have a look at these in a bit more detail:

  (cont(0)(v4:i64) (br return(v4:i64)))
  (cont(1)() (let v5:i64 = (i64.const 1)) (br 0(v5:i64)))
  (cont(2)() (let v6:i64 = (i64.const 2)) (br 0(v6:i64)))

Continuation 0 (cont(0)) takes a single argument (v4:i64) and in its body branches to the return label (meaning returning from the function), returning variable v4. This is the continuation evaluated after either branch of the if construct. The parameter records the value of the res local variable, which is modified in each branch.

Continuations 1 and 2 denote the true and false branches of the if statement, respectively. Both let-bind an integer, before branching to continuation 0.

The if construct is also quite different:

(if v3:i64 1() 2())

This can be read as “if v3 is true, then evaluate continuation 1 with no arguments, otherwise evaluate continuation 2 with no arguments”.

The generation of Stackless IR can also be performed in a single pass. WebAssembly’s validation rules allow us to know the layout of the stack at any given time, so it’s possible to emulate a stack as we pass through the list of instructions. As we name $i1 and $i2 as v1 and v2, we can keep track of the stack as follows:

(get_local $i1) ;; [v1]
(get_local $i2) ;; [v2, v1]
(i64.eq)        ;; []

which may then be translated as

(i64.eq v1 v2)

Let’s have a look at our iterative Fibonacci example in Stackless form. No need to go through it all; we’ll pick out the interesting bits below.

(fun 0 (param v0 i64) (result i64)
  ;; Initialise all local variables to 0
  (let v1:i64 = (i64.const 0))
  (let v2:i64 = (i64.const 0))
  (let v3:i64 = (i64.const 0))
  (let v4:i64 = (i64.const 0))

  ;; Initial value of i1
  (let v5:i64 = (i64.const 0))

  ;; Initial value of i2
  (let v6:i64 = (i64.const 1))

  ;; Check whether n = 0
  (let v7:i64 = (i64.const 0))
  (let v8:i64 = ((i64.eq) v0:i64 v7:i64))

  ;; Continuation 0: Evaluated if n != 0
  (cont(0)()
    ;; Check whether n = 1
    (let v9:i64 = (i64.const 1))
    (let v10:i64 = ((i64.eq) v0:i64 v9:i64))

    ;; Continuation 1: Evaluated if n != 1
    (cont(1)()
      (let v11:i64 = (i64.const 2))

      ;; Continuation 2: Evaluated if counter = n
      (cont(2)(v12:i64 v13:i64 v14:i64 v15:i64)
        (let v16:i64 = ((i64.add) v13:i64 v14:i64))
        (br return(v16:i64))
      )

      ;; Continuation 3: Loop.
      ;; 4 parameters: Counter, i1, i2, tmp
      (rec_cont(3)(v17:i64 v18:i64 v19:i64 v20:i64)
        ;; Check if counter < n
        (let v21:i64 = ((i64.lt_s) v17:i64 v0:i64))
        ;; Continuation 4: Evaluated if counter < n
        (cont(4)()
          ;; i1 + i2
          (let v22:i64 = ((i64.add) v18:i64 v19:i64))
          ;; counter ++
          (let v23:i64 = (i64.const 1))
          (let v24:i64 = ((i64.add) v17:i64 v23:i64))
          ;; Loop with new i1, i2, counter, tmp
          (br 3(v24:i64, v19:i64, v22:i64, v22:i64))
        )
        ;; If counter < n, then perform swapping. Otherwise, branch to
        ;; continuation 2.
        (if v21:i64 4() 2(v17:i64, v18:i64, v19:i64, v20:i64))
      )
      ;; Start looping, with the initial values for counter, i1, i2, and tmp
      (br 3(v11:i64, v5:i64, v6:i64, v4:i64))
    )
    ;; Continuation 5: Evaluated if n == 1. Returns 1.
    (cont(5)() (let v25:i64 = (i64.const 1)) (br return(v25:i64)))
    ;; If n == 1, return 1. Otherwise, branch to continuation 2.
    (if v10:i64 5() 1())
  )

  ;; Continuation 6: Evaluated if n == 0. Returns 0.
  (cont(6)() (let v26:i64 = (i64.const 0)) (br return(v26:i64)))
  ;; If n == 0, evaluate continuation 6. Otherwise, proceed to the rest
  ;; of the program (continuation 0).
  (if v8:i64 6() 0())
)

Perhaps the most interesting part of this translation is the loop:

(rec_cont(3)(v17:i64 v18:i64 v19:i64 v20:i64)
  ;; Check if counter < n
  (let v21:i64 = ((i64.lt_s) v17:i64 v0:i64))
  ;; Continuation 4: Evaluated if counter < n
  (cont(4)()
    ;; i1 + i2
    (let v22:i64 = ((i64.add) v18:i64 v19:i64))
    ;; counter ++
    (let v23:i64 = (i64.const 1))
    (let v24:i64 = ((i64.add) v17:i64 v23:i64))
    ;; Loop with new i1, i2, counter, tmp
    (br 3(v24:i64, v19:i64, v22:i64, v22:i64))
  )
  ;; If counter < n, then perform swapping. Otherwise, branch to
  ;; continuation 2.
  (if v21:i64 4() 2(v17:i64, v18:i64, v19:i64, v20:i64))
)

The first thing to note here is the rec_cont label, meaning that it’s possible to branch to continuation 3 from within itself. The second thing to note is that continuation 3 takes four parameters: this is because we compile away local variables, and instead pass immutable, let-bound variables as parameters.

Cmm Compilation

Now, we get to the final step of the pipeline: targeting OCaml’s Cmm backend.

Cmm?

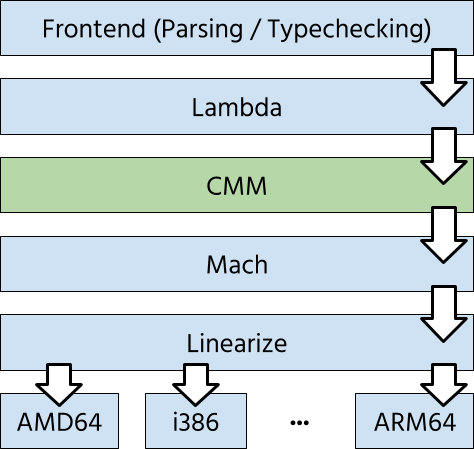
OCaml has several intermediate representations: the frontend gets translated into the various Lambda representations, which essentially provide an untyped lambda calculus.

The CLambda representation is then translated into Cmm, which is a first-order, expression-based language with support for external calls and memory access, and is the final representation before things begin to look like assembly code. Note that Cmm is not the C-- representation found in GHC.

We targeted Cmm essentially because the Lambda representations were just a bit too high-level, but we wanted to use the infrastructure such as linearisation and register allocation without implementing it ourselves.

From Stackless to Cmm

A large amount of the work in compiling to Cmm comes from implementing the various arithmetic primitives. A few key points:

• Cmm only provides word-length (in our case, 64-bit) native integers. That said, it’s easy to emulate 32-bit integers with 64-bit integers as long as the high 32 bits are cleared before operations where they become significant (for example, division or population count).

• Cmm does not support 32-bit floats. It’s not possible to emulate 32-bit floats using 64-bit floats directly. The current 32-bit float implementation is a bit of a hack: essentially, we trick Cmm into believing that it’s holding the bit pattern for a 64-bit float instead of a 32-bit float. Then, we use a result showing that double rounding is innocuous which states that converting to a 64-bit float, performing an operation, then converting back, does not introduce double rounding errors.

  An alternative would be to call out to the RTS and do the 32-bit floating point arithmetic in C.

• Cmm only provides signed integer operations. Thankfully, however, it does provide pointer comparisons (which are unsigned), and signedness does not matter for addition, division, or multiplication, so we only needed to add unsigned division to Cmm.

The interesting bit of the compilation, however, relies on Cmm’s “static exceptions” mechanism. As an example, consider the following piece of code:

(fun safe_div (x: int y: int)
  (catch
    (if (== y 0) (exit div_zero) (/ x y))
   with(div_zero) (-1)
  )
)

Here we have a “safe division” function, which checks to see whether or not the divisor is zero before performing the division. If the divisor is zero, then the exit primitive jumps to the div_zero handler, which returns -1. Otherwise, x / y is calculated as normal.

For more information on static exceptions, check out this blog post by Alain Frisch.

Static exceptions allow structured jumps. It turns out that this construct is precisely what we need in order to implement all of WebAssembly’s structured control flow functionality!

Recall our earlier example in Stackless form, where we check the equality of two numbers, returning 1 if they are equal and 0 if not:

(fun (param v0:i64) (param v1:i64) (result i64)
  (let v2:i64 = (i64.const 0))
  (let v3:i64 = ((i64.eq) v0:i64 v1:i64))
  (cont(0)(v4:i64) (br return(v4:i64)))
  (cont(1)() (let v5:i64 = (i64.const 1)) (br 0(v5:i64)))
  (cont(2)() (let v6:i64 = (i64.const 2)) (br 0(v6:i64)))
  (if v3:i64 1() 2())
)

And here is the function compiled to Cmm:

(function compare_funcinternal_0
  (v0:i64: int v1:i64)
  (catch
    (catch
      (catch (if (!= (== v0:i64 v1:i64) 0) (exit 1) (exit 2))
      with(2) (exit 0 2))
    with(1) (exit 0 1))
  with(0 v4:i64: int) v4:i64))

The key point to note is the translation of continuations. Where before continuations were just instructions, we compile cont and rec_cont instructions by compiling the remainder of the instructions as the body of the catch block, and the continuation as a handler. Thus, it’s possible to jump out to the continuation as required.

You may have also noticed that the redundant let bindings have gone: this is because we perform constant folding during Cmm compilation.

Now, we can have a look at our final compiled iterative Fibonacci example:

(function fib_dash_iter_dash_desugared_funcinternal_0
     (v0:i64: int fuel: int)
 (try
   (if (<= fuel 0) (raise_notrace 7)
     (catch
       ;; if (n == 0) { return 0; }
       (catch (if (!= (== v0:i64 0) 0) (exit 6) (exit 0)) with(6) 0)
     with(0)
       (catch
         ;; if (n == 1) { return 1; }
         (catch (if (!= (== v0:i64 1) 0) (exit 5) (exit 1)) with(5) 1)
       with(1)
         (catch
           ;; Exit to branch 3
           ;; Counter = 2
           ;; i2 = 0
           ;; i1 = 1
           ;; tmp = 0
           (catch rec (exit 3 2 0 1 0)
           with(3 v17:i64: int v18:i64: int v19:i64: int v20:i64: int)
             (catch
               ;; if (counter < n) { exit(4) }
               ;; else { exit(2) }
               (if (!= (< v17:i64 v0:i64) 0) (exit 4)
                 (exit 2 v17:i64 v18:i64 v19:i64 v20:i64))
             with(4)
               ;; tmp = i1 + i2
               (let v22:i64 (+ v18:i64 v19:i64)
                 ;; loop with counter +1, i1 = i2, i2 = tmp, tmp = tmp
                 (exit 3 (+ v17:i64 1) v19:i64 v22:i64
                   v22:i64))))
         with(2 v12:i64: int v13:i64: int v14:i64: int v15:i64: int)
           ;; return i1 + i2
           (+ v13:i64 v14:i64)))))
 with reason (extcall "wasm_rt_trap" reason int)))

First, note the additional fuel parameter and the check to see whether it is less then zero – this is because the WASM specification requires that a trap (uncatchable exception) is raised in the case of too many nested calls.

Second, we can actually begin to see the structure of the original code a little better, now that the catch blocks are sequenced a bit better. We do the first two checks, returning 0 or 1 respectively if necessary and branching otherwise. Next, we enter the recursive catch block with the initial values 2 0 1 0: 2 is the initial counter, 0 is the initial i1, 1 is the initial i2, and 0 is the initial tmp. If the counter value is less than n, then we branch to 4 which performs the swaps with i1 and i2 and loops. Otherwise, we branch to block 2 and return i1 + i2.

Runtime System

We require a lightweight runtime system to supplement the compiled code. The RTS is largely the same as the wasm2c RTS, with a few modifications and extensions. Here are the main points:

1. Traps: Traps are raised when an unrecoverable fault (such as unreachable code being evaluated, or an out-of-bounds memory access occurring) happens, and aborts execution. The RTS handles traps through the use of setjmp / longjmp in C.

2. Linear memory: the RTS handles memory allocation and initialisation. It can do this either by malloc and explicit bounds checks, or via mmaping a large chunk of memory and handling segmentation faults by raising a trap on out-of-bounds accesses. Explicit bounds checks slow down the code a lot.

3. Tables: the RTS allocates a chunk of memory used for function tables (although the vast majority of the logic for actually performing indirect calls is compiled).

4. Primitives unsupported in Cmm: while I’ve endeavoured to compile as much as I can in Cmm, extending it where necessary, some bits of functionality (for example, f32 conversions) just are’t readily available, and consequently are implemented via a C call to the RTS.

Emscripten Support

Emscripten is a mature compiler from C to WebAssembly. Since Emscripten is the primary way to generate WebAssembly code, it would be useful to support it.

Emscripten has a fairly robust runtime system which allows it to emulate many system calls, standard library functions, and even external library functions. The Emscripten RTS also performs its own memory management through compiled versions of malloc and a custom stack layout using linear memory. To get Emscripten programs running, it’s necessary to port this infrastructure over to C, which I have started doing here. It’s still very much a work in progress, but the memory management seems to work, and I’ve managed at least to get the entire PolyBenchC benchmark suite compiling and running correctly.

Optimisations

Many of the optimisations in the OCaml compiler occur prior to the Cmm level. In any case, we implement some heavy-hitting ones ourselves quite easily: constant propagation / folding; dead code elimination, and simple inlining.

The OCaml backend provides a finer-grained dead code elimination pass, as well as common subexpression elimination.

Evaluation

WASM Test Suite

WebAssembly has a battery of tests to check whether an implementation conforms to the specification. We pass this test suite in its entirety.

Performance Evaluation

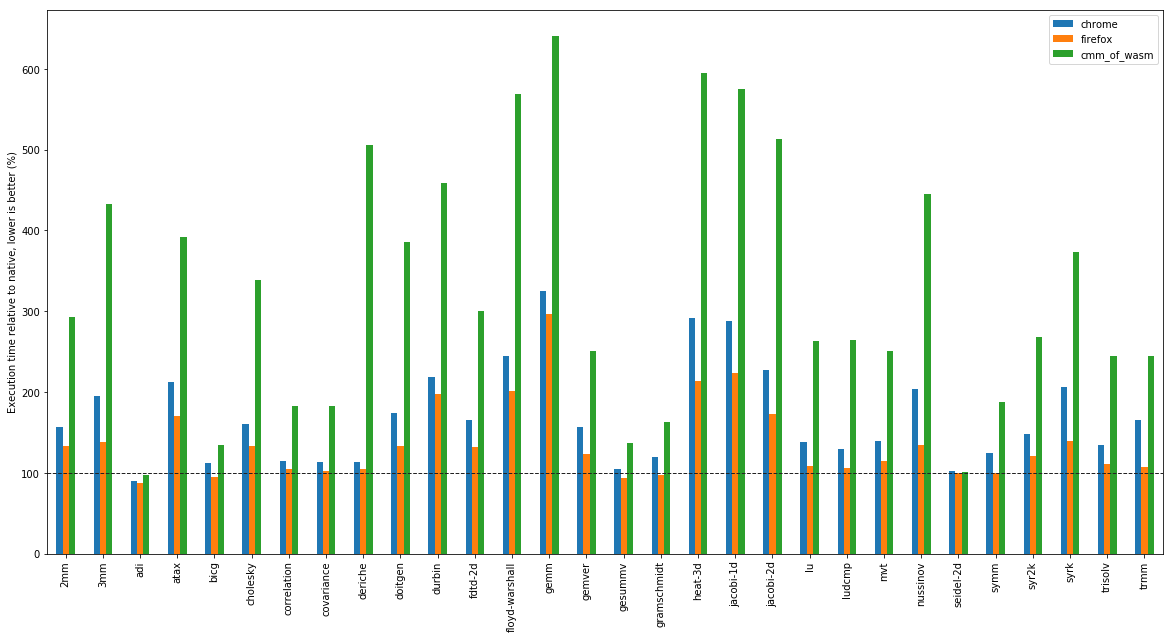
Finally, let’s see some preliminary performance numbers.

Like the original WebAssembly paper, we ran the various implementations on the PolyBenchC benchmark suite. Each benchmark was compiled using Emscripten -O3 1.38.10, run 15 times (discounting a run on the JITs to account for warmup time), and the value reported is the arithmetic mean normalised to native code execution. The machine used was a quad-core Intel Core i5 CPU running at 3.20GHz, with 16GB of RAM.

There are three experimental cases: V8, running through Chromium 68.0.3440.106; SpiderMonkey, running through Firefox 61.0.2; and cmm_of_wasm, using the OCaml graph colouring register allocator (although the linscan allocator gives similar results). We use the time reported by PolyBenchC’s internal timer, which doesn’t include VM startup time.

The above graph shows performance relative to native code (see the dashed line). In some cases, we do really well: adi and seidel-2d are both close to native. In some cases, we do quite badly: whereas both Chrome and Firefox get close to native performance in deriche, we see a 5X slowdown compared to native.

All in all, there’s still a bit of work to do to get cmm_of_wasm closer to production implementations. That said, in all cases, the compiler produces code which performs within an order of magnitude of native code; and which is generally 2-3x slower than production JIT implementations. The optimisations we’ve done are quite simple: there is still scope for plenty more.

Conclusion

In this post, I’ve introduced cmm_of_wasm, which introduces a functional spin on WebAssembly compilation by compiling to a continuation-based IR, and targeting OCaml’s CMM backend.

There are a few directions to take next:

1. Enhancing Emscripten support: our implementation of the Emscripten RTS as it stands is rather limited: it would be good to implement a larger number of syscalls and APIs.

2. Further optimisations: the compiler implements some basic optimisations, but to get more performant code, it would be good to support more advanced optimisations, in particular loop-based optimisations.

3. Prototype some WebAssembly extensions, in particular the GC proposal

4. Formalise the various IRs and compilation steps, as a stepping stone to verified WebAssembly compilation.

Acknowledgements

Thanks to KC Sivaramakrishnan and Stephen Dolan for supervising this work, and to Mark Shinwell, Pierre Chambart, and Sander Spies for useful technical discussions.

Special thanks to Pierre Chambart, who came up with an initial design for the Stackless IR, and who shared an initial prototype.

This work was funded by an internship at OCaml Labs, who also provided a wonderful working environment.

Finally, thanks to Sam Lindley and Maria McParland for comments on a draft version of this post.